SICP. Foreword–1.1.
2022-11-02 Wed

• ``You type an expression, and the interpreter responds by displaying the result of its evaluating that expression.''
• Combinations;
• Operator;
• Operands;
• Arguments.
• read-eval-print loop: ``the intepreter always operates in the same basic cycle: It reads an expression from the terminal, evaluates the expression, and prints the result''.

• A programming language provides means to use names to refer to computational object. ``We say that the name identifies a variable whose value is the object.''
• `` Define is our language's simples means of abstraction.
• Environment.

• The interpreter evaluates combinations by following a procedure:

  • To evaluate a combination, do the following:
    1. Evaluate the subexpressions of the combination;
    2. Apply the procedure that is the value of the leftmost subexpression (the operator) to the arguments that are the values of the other subexpressions (the operands).

• The evaluation rule is recursive.

• We can view the evaluation in terms of a tree (See p. 10).

  

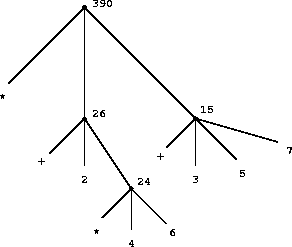
• Tree accumulation.
• Special forms constitute exceptions to the general evaluation rule. Define is a special form.

• Procedure definitions: a much more powerful abstraction technique.
• Compound procedures.

• Application process for compound procedures:
  • To apply a compound procedure to arguments, evaluate the body of the procedure with each formal parameter replaced by the corresponding argument.
• Substitution model for procedure application: a model to determine the ``meaning'' of procedure application (in this chapter);
  • This is not how interpreters actually work;
  • The substitution model is the first of a sequence of increasingly elaborated models presented in this book of how intepreters work. Chapter 5 will present a complete implemetation of an interpreter an compiler.
• Lisp uses applicative-order evaluation: the interpreter evaluates the operator and the operands and then applies the resulting procedure to the resulting arguments — the procedure (followed by the intepreter to evaluate a combination) described above.
• An alternative evaluation mode: normal-order evaluation.

• cond
• if
• and
• or
• not

Exercise:

Below is a sequence of expressions. What is the result printed by the interpreter in response to each expression? Assume that the sequence is to be evaluated in the order in which it is presented.

10
(+ 5 3 4)
(- 9 1)
(/ 6 2)
(+ (* 2 4) (- 4 6))
(define a 3)
(define b (+ a 1))
(+ a b (* a b))
(= a b)
(if (and (> b a) (< b (* a b)))
    b
    a)
(cond ((= a 4) 6)
      ((= b 4) (+ 6 7 a))
      (else 25))
(+ 2 (if (> b a) b a))
(* (cond ((> a b) a)
         ((< a b) b)
         (else -1))
   (+ a 1))

Answer:

10
;; 10

(+ 5 3 4)
;; 12

(- 9 1)
;; 8

(/ 6 2)
;; 3

(+ (* 2 4) (- 4 6))
;; 6

The authors, p. 8 fn. 8, say that the response to evaluating definitions is ``highly implementation-dependent''.

I gather that Scheme's define, when used for variables, is equivalent for Elisp's setq.

(setq a 3)
;; 3

(setq b (+ a 1))
;; 4

(+ a b (* a b))
;; 19

I gather that Scheme's =, when used for variables, is equivalent for Elisp's eq.

(eq a b)
;; nil

(if (and (> b a) (< b (* a b)))
    b
  a)
;; 4

(cond ((= a 4) 6)
      ((= b 4) (+ 6 7 a))
      (else 25))
;; 16

(+ 2 (if (> b a) b a))
;; 6

(* (cond ((> a b) a)
         ((< a b) b)
         (else -1))
   (+ a 1))
;; 16

Exercise:

Translate the following expression into prefix form

\(\frac{5 + 4 + (2 - (3 - (6 + \frac{4}{5})))}{3(6 - 2)(2 - 7)}\)

Answer:

(/ (+ 5 
      4 
      (- 2
         (- 3
            (+ 6
               (/ 4 5))))) 
   (* 3 
      (- 6 2) 
      (- 2 7))) 

Exercise:

Define a procedure that takes three numbers as arguments and returns the sum of the squares of the two larger numbers.

Answer:

This was my first solution:

(defun foo (a b c)
  (+ (square (if (> a b) a b))
     (square (if (> c
                    (if (> a b) b a))
                    c
                    (if (> a b) b a)))))

That works, although it is not ideal, because the combination (> a b) is evaluated three times…

Exercise:

Observe that our model of evaluation allows for combinations whose operators are compound expressions. Use this observation to describe the behavior of the following procedure:

(define (a-plus-abs-b a b)
  ((if (> b 0) + -) a b))

Answer:

Behavior: If b is greater than 0, then apply + to a and b, that is, add b to a. Otherwise, apply - to a and b, that is, to subtract b from a.

But subtracting a negative number, means adding it! So, behavior: Add the absolute value of b to a.

Exercise:

Ben Bitdiddle has invented a test to determine whether the interpreter he is faced with is using applicative-order evaluation or normal-order evaluation. He defines the following two procedures:

(define (p) (p))

(define (test x y)
  (if (= x 0)
      0
      y))

Then he evaluates the expression

(test 0 (p))

What behavior will Ben observe with an interpreter that uses applicative-order evaluation? What behavior will he observe with an interpreter that uses normal-order evaluation? Explain your answer. (Assume that the evaluation rule for the special form if is the same whether the interpreter is using normal or applicative order: The predicate expression is evaluated first, and the result determines whether to evaluate the consequent or the alternative expression.)

Answer:

In the case of applicative-order evaluation, ``the interpreter first evaluates the operator and operands and then applies the resulting procedure to the resulting arguments'' (p. 16). This means that the interpreter will evaluate test, then 0 and then (p). test evaluates to a procedure. 0 evaluates to 0. But (p) evaluates to (p), which evaluates to (p), which evaluates to (p)', which… ad infinitum. So, the interpreter enters an infinite evaluation; it will never be able to apply the procedure denoted by test, because it will never be able to compute the second argument.

In the case of normal-order evaluation, operands are not evaluated until their values are needed. (test 0 (p)) would be turned into 0 and then evaluated. And '0' evaluates to 0.

• Procedures are analogous to mathematical functions: ``[t]hey specify a value that is determined by one or more parameters''. (21-22)
• However, procedures are different from mathematical functions in some respects. A mathematical function can tell us, say, whether a certain number is the square root of x or not. That, however, does not describe a procedure. It does not tell us how to find the square root of x.
• More generally, mathematics is usually concerned with ``declarative knowledge'', whereas computer science is concerned with ``imperative knowledge''.
• Iteration can be accomplished by calling a procedure. We don't need any looping construct.

Exercise:

Alyssa P. Hacker doesn't see why if needs to be provided as a special form. ``Why can't I just define it as an ordinary procedure in terms of cond?'' she asks. Alyssa's friend Eva Lu Ator claims this can indeed be done, and she defines a new version of if:

(define (new-if predicate then-clause else-clause)
  (cond (predicate then-clause)
        (else else-clause)))

Eva demonstrates the program for Alyssa:

(new-if (= 2 3) 0 5)
5

(new-if (= 1 1) 0 5)
0

Delighted, Alyssa uses new-if to rewrite the square-root program:

(define (sqrt-iter guess x)
  (new-if (good-enough? guess x)
          guess
          (sqrt-iter (improve guess x)
                     x)))

What happens when Alyssa attempts to use this to compute square roots? Explain.

Answer:

cond is a special form. if, too, is a special form. new-if, instead, is not a special form. It is an ordinary combination.

Now, the evaluation of a combination entails the evaluation of both the operator and the operands. With Eva's new-if, then, sqrt-iter calls itself ad infinitum and a stack overflow occurs.

In fact, if we replace the new-if — a combination — with the cond — a special form — it would evaluate to, then things will work as originally intended.

The good-enough? test used in computing square roots will not be very effective for finding the square roots of very small numbers. Also, in real computers, arithmetic operations are almost always performed with limited precision. This makes our test inadequate for very large numbers. Explain these statements, with examples showing how the test fails for small and large numbers. An alternative strategy for implementing good-enough? is to watch how guess changes from one iteration to the next and to stop when the change is a very small fraction of the guess. Design a square-root procedure that uses this kind of end test. Does this work better for small and large numbers?

Answer:

This is a pretty small number: \(0.00025\). It's square root is \(\sqrt{0.00025} = 0.0158113883\) (I have used a calculator).

Let's try to apply our test to the right answer divided by two.

(good-enough? (/ 0.0158113883 2) 0.00025)

The test returns true; that is, it's telling us that half of the right answer is good enough. I take that as a failure.

When we are dealing with very small numbers, then the \(0.001\) used in our test is too big for our purposes.

This is a pretty big number: \(7894561230.0123456789\). The square root of this number is \(\sqrt{7894561230.0123456789} = 88851.3434339\) (I have used a calculator).

Let's see whether are test consider the right answer as good enough…

(good-enough? 88851.3434339 7894561230.0)

This evaluate to nil… The problem seems to lie in the application of (the procedure named by) square, which gives a rather imprecise result.

This is the body of good-enough?:

(< (abs (- (square 88851.3434339) 7894561230.0)) 0.001)

It evaluates to nil, because the difference between the square of the guess and the radicant is greater than 0.001. However, the actual square of the radicant does not differ from the radicant of a value greater than 0.001.

Here is my version of an improved version of good-enough? following the authors' suggestion:

(defun good-enough-improved? (new-guess old-guess)
  (< (abs (- (abs old-guess) (abs new-guess))) (/ old-guess 10000000.0)))

(defun sqrt-iter2 (new-guess old-guess x)
  (if (good-enough-improved? new-guess old-guess)
      new-guess
    (sqrt-iter2 (improve new-guess x) new-guess x)))

(defun sqrt2 (x)
  (sqrt-iter2 1.0 x x))

My version seems to work much better for small numbers:

(sqrt 0.00025) ;; => 0.033869844451165365
               ;;    bad!
(sqrt2 0.00025) ;; => 0.015811388300841896
                ;;    As good as the built-in emacs lisp sqrt function!

But there doesn't seem to be difference with big numbers:

(sqrt 7894561230.0)  ;; 88851.34343385023
(sqrt2 7894561230.0) ;; 88851.34343385023

This is so, I think, because, even if good-enough? returns nil when it shouldn't, improve is called until we get something that differs from the radicant for less than 0.001… is this correct?

Exercise:

Newton’s method for cube roots is based on the fact that if \(y\) is an approximation to the cube root of \(x\), then a better approximation is given by the value \(\frac{x/y^2 + 2y}{3}\). Use this formula to implement a cube-root procedure analogous to the square-root procedure. (In 1.3.4 we will see how to implement Newton’s method in general as an abstraction of these square-root and cube-root procedures.)

Answer:

(defun cuberoot (x)
  (cuberoot-iter2 1.0 x x))

(defun cuberoot-iter (new-guess old-guess x)
  (if (good-enough-improved? new-guess old-guess)
      new-guess
    (cuberoot-iter2 (improve-cr new-guess x) new-guess x)))

(defun improve-cr (guess x)
  (/ (+ (/ x (square guess))
        (* 2 y))
     3))

• Procedural abstraction.
• Bound variables.
• Free variables.
• Block structure.
• Lexical scoping.